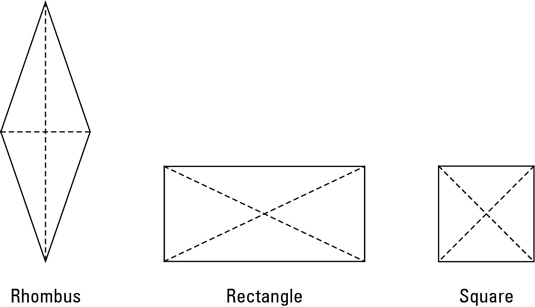
All the properties of a rhombus apply the ones that matter here are parallel sides diagonals are perpendicular bisectors of each other and diagonals bisect the angles. In a rhombus the diagonals bisect each other.
 Properties Of Rhombuses Rectangles And Squares Dummies
Properties Of Rhombuses Rectangles And Squares Dummies
All the properties of a rhombus apply the ones that matter here are parallel sides diagonals are perpendicular bisectors of each other and diagonals bisect the angles.
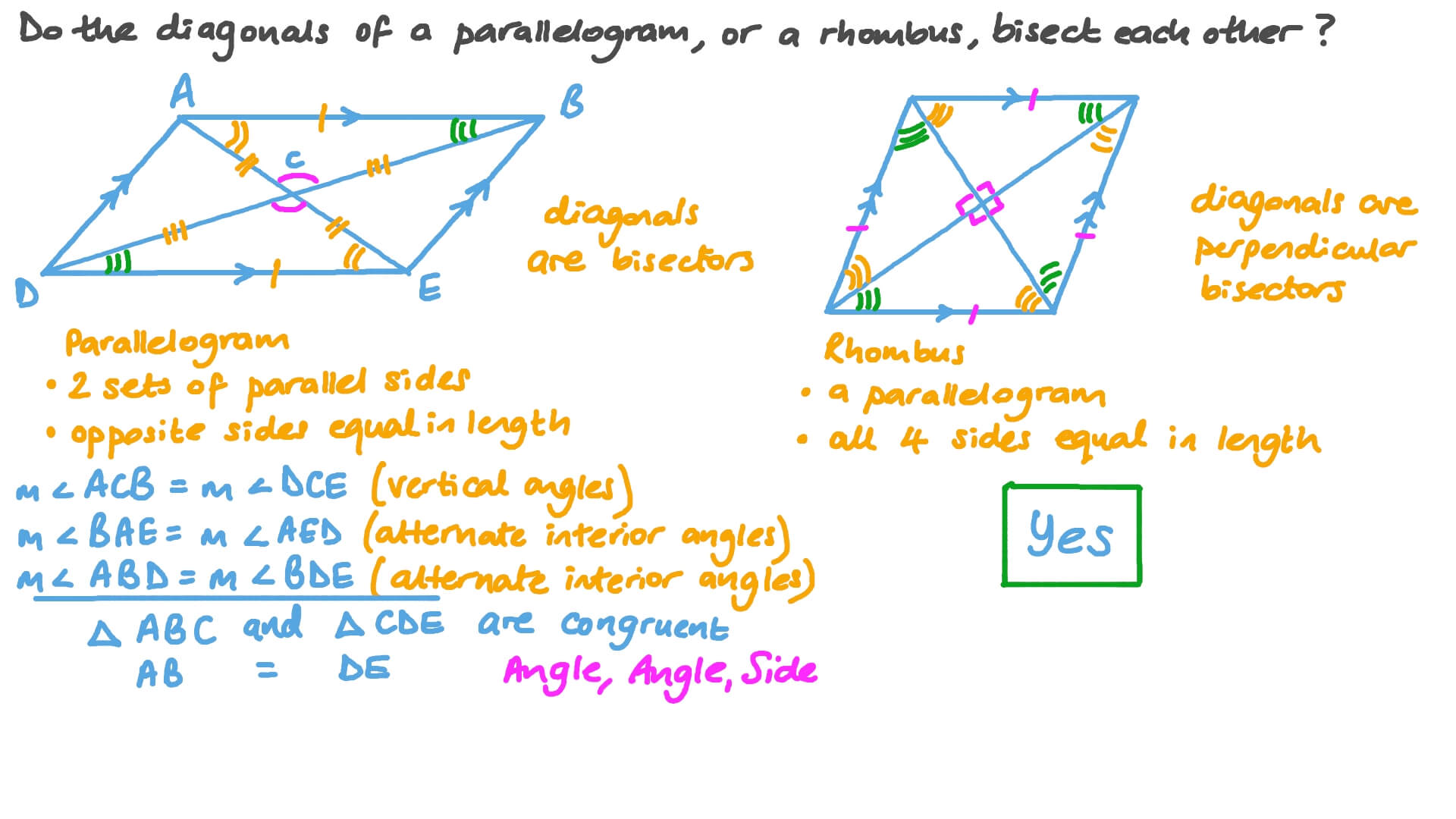
Does a rhombus have congruent diagonals. The four sides are already all congruent. Opposite angles in a rhombus are already congruent. In any rhombus the diagonals lines linking opposite corners bisect each other at right angles 90.
H The sum of the four interior angles is 4 right angles. That is each diagonal cuts the other into two equal parts and the angle where they cross is always 90 degrees. C The longer diagonal of a rhombus is.
Hence the word best describes a parallelogram with diagonals that are congruent and perpendicular would be Square. Click to see full answer. Which attribute is not always true for a rhombus.
A rhombus with congruent diagonals will be a square. Which attribute is not always true for a rhombus. Two pairs of opposite sides are.
Opposite angles are congruent. Having the diagonals congruent forces all of the angles to be congruent as well. K Join the mid-points of the half the diagonals in order and you get a rhombus.
Every rhombus is a kite and any quadrilateral that is both a kite and parallelogram is a rhombus. Which is an example of a quadrilateral whose diagonals are congruent but do NOT bisect each other. I The two diagonals form four congruent right angled triangles.
Get an answer to your question Which property is always true for a rhombus but not always true for a parallelogram. Though the diagonals of a rhombus do have special properties such as intersecting at. Yes a square is a rhombus A square must have 4 congruent sides.
A rhombus is a square. Posted on February 13 2021 by. When diagonals of a parallelogram are congruent and perpendicular then it is a squareIf diagonals are just perpendicular then we call it a rhombusIf diagonals are just congruent then we call it a rectangle.
Rhombus the diagonals lines linking opposite corners bisecteach other at right angles 90. Opposite sides are congruent. Motivación La motivación es un factor importante al emprender un negocio tanto para el emprendedor como para la gente que colabora con el en su proyecto en esta sección presentaremos diferentes materiales para ayudar a impulsar esa parte.
If this were the case it would be a square which technically can be classified as a rhombus. In the figure above drag any vertex to reshape the rhombus and convince your self this is so. Squares have diagonals that bisect the angles.
Rhombus A parallelogram with four sides of equal length. The diagonals are congruent. Creatividad No siempre es fácil generar esas ideas de negocios necesarias para poder emprender.
Rhombi do not have congruent diagonals but they do bisect each other. Diagonals are congruent. A parallelogram must be a rhombus if the.
January 25 2021 Like a parallelogram opposite angles of a rhombus are congruent. In a rhombus both pairs of opposite sides are congruent. A simple non-self-intersecting quadrilateral is a parallelogram if and only if any one of the following statements is true.
J Join the mid-points of the sides in order and you get a rectangle. That is each diagonal cuts the other into two equal parts and the angle where they cross is always 90 degrees. Every rhombus has 4 congruent sides so every single square is also a rhombus.
See full answer below. Do Squares have diagonals that bisect the angles. Emprendedores Motivación Creatividad Social y más.
Square A parallelogram with four sides of equal length and angles of equal size right angles. All sides are congruent by definition. The square has the following properties.
With one exception the diagonals of a rhombus are NOT congruent. All the properties of a rectangle apply the only one that matters here is diagonals are congruent. All the properties of a rectangle apply the only one that matters here is diagonals are congruent.
Two pairs of opposite sides are parallel by definition. Become a member and.
Parallel And Perpendicular Lines Gcse Math Teaching Geometry Studying Math. Kellys Proof Statement Justification 2 4 Vertical angles are congruent.
 How To Prove Angles Are Complementary Or Supplementary Dummies
How To Prove Angles Are Complementary Or Supplementary Dummies
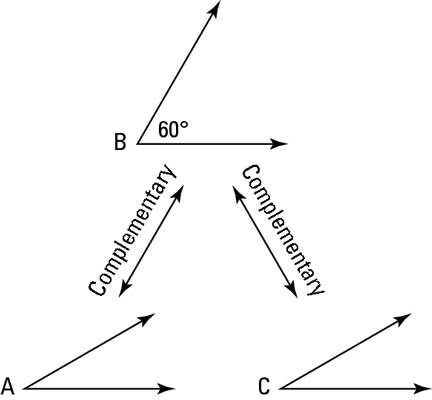
These angles arent the most exciting things in geometry but you have to be able to spot them in a diagram and know how to use the related theorems in proofs.

Congruent and supplementary angles. Consider the diagram below. Lets add some tools to our geometry tool belt. Reiterate how two supplementary angles make a straight angle.
Median response time is 34 minutes and may be longer for new subjects. Ashtyn and Hannah helping you with Supplementary and Congruent Angles involving Parallel lines. So let me write that down.
1 3 Vertical angles are congruent. Since angle B is supplementary to both angles C and D either of these angle measures may be used to determine the measure of Angle B. Angle DBA and angle ABC are supplementary.
Thus if one of the angle is x the other angle will be 90 x For example in a right angle triangle the two acute angles are complementary. Response times vary by subject and question complexity. The intersections of a transversal with two lines create various types of pairs of angles.
Y 1 y-3x2 -10- 2 y-3x6 1. Angles from each pair of vertical angles are known as adjacent angles and are supplementary the angles sum up to 180 degrees. Sum of the angles in a triangle is 180 degree worksheet.
For example the angles whose measures are 112 and 68 are supplementary to each other. Once again lets say that this is 50 degrees. Upon close observation its revealed that two intersecting lines give rise to four linear pairs too.
Heres a thorough explanation of complementary and supplementary angles as well as definitions of adjacent a. Sum of two complementary angles 90. In fact the only time they are congruent meaning they have the same measure is when the.
Since one angle is 90 the sum of the other two angles forms 90. Finding Supplementary Angles - Type 2. Vertical angles are congruent.
How to find supplementary angles. Play this game to review Mathematics. Ie POR ROQ 50 o 130 o 180 o.
Using the measure of either angle C or angle D we find the measure of angle B to be 180 180 x 180 180 x x. Vertical Angle Theorem Daniels Proof Statement Justification 1 2 180 Definition of Supplementary Angles 1 4 180 Definition of Supplementary Angles 1. Angle 1 27 o Find the measure of angle 4.
I already used C. Alternate Interior Angles Alternate Exterior Angles Corresponding Angles Same-Side Interior Angles supplementary. Both angle C and angle D have measures equal to 180 x and are congruent.
Powered by Create your own unique website with customizable templates. Which of the following is an equation for the line shown below. So they are supplementary.
But the angles don. Since sum of the these two angles are 180 o. Supplementary Angles Two angles are said to be supplementary to each other if sum of their measures is 180.
When two lines intersect two pairs of congruent angles are formed. Two supplementary angles add up to 180 or a straight angle. From the above example POR 50 o ROQ 130 o are supplementary angles.
Get your students to skillfully find supplementary pairs match the angles and follow the rules of the given in-out box for correct answers. If any angle of Y is less than 180 o then. It is known that AE62 AN 5b.
And are on the same side of the transversal. And lets say that this right over here is 130 degrees. So the same side interior angles.
Our printable vertical angles worksheets for grade 6 grade 7 and grade 8 take a shot at simplifying the practice of these congruent angles called vertically opposite angles. Complementary angles are two angles that add up to 90 or a right angle. Here POR is said to be supplementary angle of ROQ and ROQ is said to be supplementary angle of POR.
Clearly angle DBA plus angle ABC if you add them together you get 130 degrees plus 50 degrees which is 180 degrees. Same side interior angles are congruent. This is because in a triangle the sum of the three angles is 180.
As a consequence of Euclids parallel postulate if the two lines are parallel consecutive interior angles are supplementary corresponding angles are equal and alternate angles are equal. Same side interior angles are not always congruent. Identify the relationship of the shown pair of angles as either congruent or supplementary.
Consecutive interior angles corresponding angles and alternate angles.
Here is what is given. In a rectangle ABCD sides AB and CD are congruent and parallel sides AD and BC are congruent and parallel all internal angles are 90o.
 Diagonals Of Rectangles Are Of Equal Length Geometry Help
Diagonals Of Rectangles Are Of Equal Length Geometry Help
As you can see a diagonal of a rectangle divides it into two right triangles BCD and.
The diagonals of a rectangle are congruent. The first way to prove that the diagonals of a rectangle are congruent is to show that triangle ABC is congruent to triangle DCB. A rectangle is a quadrilateral with four right angles. The diagonals of a square bisect each other.
The diagonals of a parallelogram_____bisect the angles. Yes since opposite angles are congruent. In the figure above click reset.
A square is_____a rhombus. The diagonals of a rectangle are perpendicular. Like a square the diagonals of a rectangle are congruent to each other and bisect each other.
The diagonals of a rectangle are congruent. The diagonals for a square are congruent. Each diagonal divides the rectangle into two congruent right triangles.
Yes and we will prove that in this video. Since ABCD is a rectangle it is also a parallelogram. Hence it proves that the diagonals of the rectangle are congruent.
If a quadrilateral is a rectangle then the diagonals of that quadrilateral are congruent. The figure below shows a rectangle ABCD having diagonals AC and DB. Image will be uploaded soon Fun Facts.
The formula to find the length of the diagonal of a rectangle is. Is a rectangle is a parallelogram. Yes the diagonals of a rectangle are always congruent because as the opposite sides of a rectangle r congruent so the diagonals must be congruent.
Segment AC segment BD. The diagonals of A B C D are congruent. The diagonals of a rectangle are_____congruent.
Sides of a rectangle are congruent. Since the diagonals of a rectangle are congruent MO 26. A quadrilateral with one pair of sides congruent and on pair parallel is_____a parallelogram.
The diagonals of a parallelogram_____bisect the angles of the parallelogram. Are the diagonals of a rectangle congruent. Proof diagonals of a rectangle are congruent is easy to demonstrate an.
A 1000 sided shape In geometry is called a chiliagon a polygon with 1000 sides The flat surfaces of many 3D geometrical figures or objects are formed of 2D shapes. Abcd has congruent diagonals. Diagonals bisect each other.
Identify the steps that complete the proof. Complete the coordinate proof of the theorem. Abcd is a rectangle.
A B C D is a rectangle. Jimmy wrote the following proof to - 7832513. Thus a rectangle has all the properties of a parallelogram.
Diagonal of a Rectangle l 2 b 2. A rectangle ABCD is shown with diagonals AC and BD. Opposite sides are parallelOpposite sides are congruent Opposite angles are congruentDiagonals bisects each other.
If a quad is a rectangle then it is a parallelogram. Opposite angles of a rectangle are congruent. Here is what you need to prove.
Length of the diagonal. Therefore triangles ΔABC and ΔABD are congruent as right triangles with one cathetus AB shared among them and another pare of catheti BC and AD being congruent. Opposite sides of a rectangle are parallel.
Also When diagonals of a parallelogram are congruent and perpendicular then it is a squareIf diagonals are just perpendicular then we call it a rhombusIf diagonals are just congruent then we call it a rectangle. A rectangle has two diagonals as it has four sides. 3 on a question.
Terfore their diagnols will also be congruent. Opposite sides of a rectangle are the same length congruent. The angles of a rectangle are all congruent the same size and measure Remember that a 90 degree angle is called a right angle So a rectangle has four right angles.
Because the triangles are congruent they have the same area and each triangle has half the area of the rectangle. Finding length of MZ. To find MZ you must remember that the diagonals of a parallelogram bisect each otherRemember a rectangle is a type of parallelogram so rectangles get all of the parallelogram properties If MO 26 and the diagonals bisect each other then MZ ½26 13.
If a diagonal bisects a rectangle two congruent right triangles are obtained. If a quad is a rectangle then it is a square.