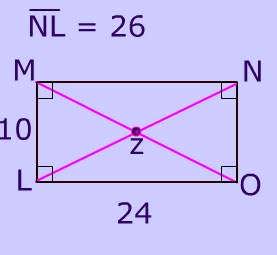
Finding length of MZ. Diagonal of a Rectangle.
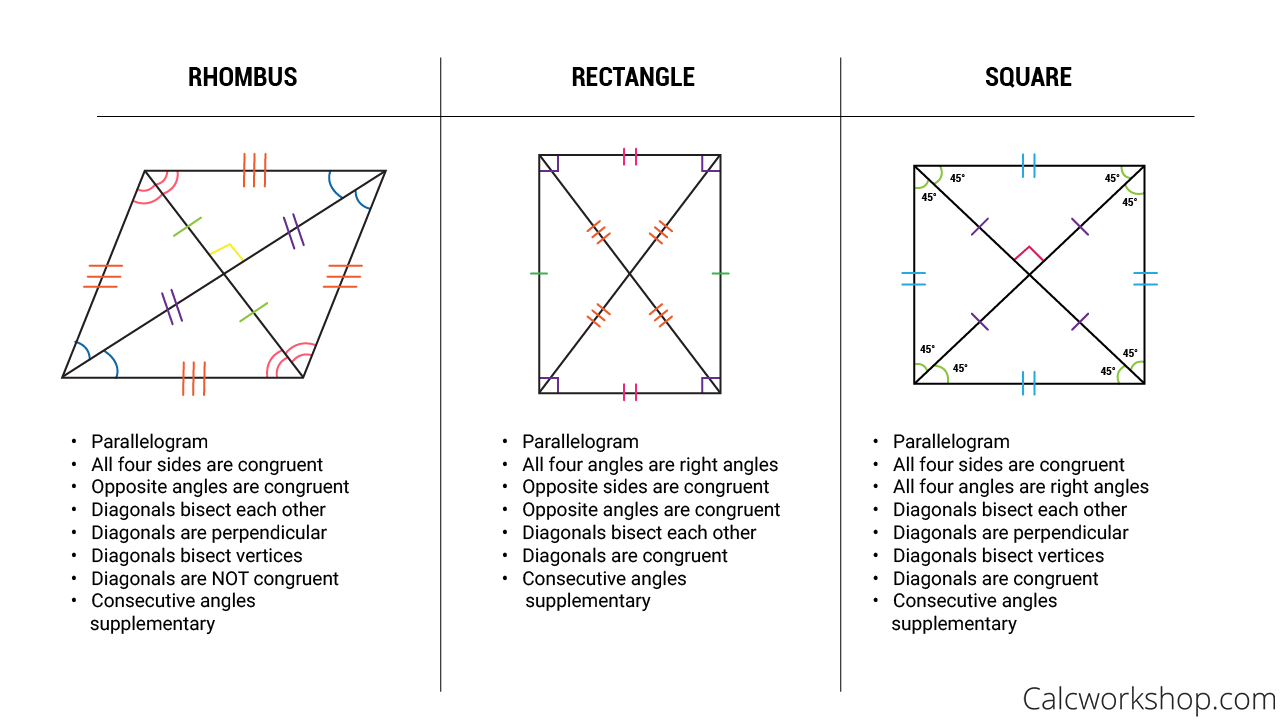Special Parallelograms 19 Step By Step Examples
The basic properties of a rectangle Rectangle can be a parallelogram rhombus or square in which all the angles right.
Properties of a rectangle diagonals. Learn how to solve problems with rectangles. Presented here are printable worksheets based on the next important property of the rectangle - the diagonals of a rectangle are congruent and bisect each other. The diagonals of a rectangle are.
Their diagonals are also congruent to each other and bisect each other. Unless the rectangle is a square And the angles formed by the intersection are not always the same measure size. All angles are right.
Since the sum of the interior angles of a polygon is. A rectangle whose two diagonals bisect each other at right angles is called a square. To find MZ you must remember that the diagonals of a parallelogram bisect each otherRemember a rectangle is a type of parallelogram so rectangles get all of the parallelogram properties If MO 26 and the diagonals bisect each other then MZ ½26 13.
On applying Pythagoras theorem in Δ ABD AB2 AD2 DB2 242 72 DB2 576 49 DB2 DB2 625 DB 25 cm Thus the length of the diagonal is 25 cm. Two congruent right triangles are obtained if the diagonal bisects a rectangle. The sum of all the interior angles is equal to 360 degrees.
The Diagonals of a Rectangle Are of Equal Length. A rectangle has two diagonals. The diagonals bisect each other.
All the angles of a rectangle are 90 Opposite sides of a rectangle are equal and Parallel. Each one is a line segment drawn between the opposite vertices corners of the rectangle. 360circ 360 it follows that each of the interior angles is a right angle.
The diagonals of a rectangle are of the same length and intersect one another The two diagonals of a rectangle intersect each other at different angles one acute angle and the other an obtuse angle. Therefore they also have two diagonals. A rectangle is a quadrilateral.
Properties of a Rectangle Opposite sides are parallel and congruent. A rectangle is a parallelogram with each of the angles a right angle. The diagonals have the following properties.
The fundamental definition of a rectangle is as follows. Rectangle formula â Area and perimeter of a rectangle. Introduction to Practical Geometry.
Diagonals that are perpendicular and congruent diagonals that bisect opposite angles consecutive angles that are supplementary. A rectangle is a parallelogram. A rectangle whose two diagonals intersect each other at right angles is known as a square.
The diagonals are congruent and bisect each other divide each other equally. Students of 5th grade and 6th grade need to apply the property to find the missing measure. Some of the properties of rectangles ar.
A rectangle has three properties. Diagonals of a rectangle bisect each other. The two diagonals are congruent same length.
Both the diagonals are equal in length. A diagonal will divide the rectangle into two right angle triangles. The diagonals of a square are perpendicular bisectors of each other.
A rectangle has two diagonals that bisects each other. A rectangle is a quadrilateral whose interior angles are all equal. In the figure above click show both diagonals then drag the orange dot at any vertex of the rectangle and convince yourself this is so.
The two diagonals of a rectangle bisect each other at different angles one obtuse angle and the other an acute angle. Each interior angle is equal to 90 degrees. The opposite sides are parallel and equal to each other.
Constructing a Quadrilateral When the Lengths of Four Sides and a Diagonal Are Given. The properties of diagonals of rectangle is hereunder. The diagonals of a rectangle are Preview this quiz on Quizizz.
The fundamental properties of rectangles are. Properties of the diagonals of a rectangle. An opposite sides of the rectangle are the same length ie.
Now let us learn the properties of rectangle in this article. The diagonals of a rectangle bisect each other and are of the same length. Rectangles are similar to squares.
Since the diagonals of a rectangle are congruent MO 26. As you can see from the pictures to the left the diagonals of a rectangle do not intersect in a right angle they are not perpendicular. Remember that a 90 degree angle is called a.
Properties of a Square. Play this game to review Geometry. In a rectangle all the angles are equal to 90º.
The rectangle is a symmetrical shape and has both the diagonals equal in length.
Examples of metals are Gold Silver Iron Uranium and Zinc. Nonmetals are elements showing less or no metallic properties.
Metals Nonmetals Metalloids
Nonmetals display some or all of the following characteristics.
Properties of metals nonmetals and metalloids. All metals have a shiny appearance at least when freshly polished. Nonmetal are poor conductors of electricity and heat. Metalloids have properties intermediate between the metals and nonmetals.
Trends based on Groups. Development of the Periodic table Effective Nuclear Charge Atomic and Ionic sizes Ionization Energy Electron Affinity Metals Nonmetals and Metalloids. Metalloids share characteristics of both metals and non-metals and are also called semimetals.
They are less conductive than metal. Metals and metalloids are generally solid at room temperature whereas nonmetals exist as liquids gases or brittle solids. Nonmetals does not reflect light.
Metalloids have properties that are between the properties of nonmetals and metals. Non-metals do not conduct heat or electricity very well. List four physical properties of metals nonmetals and metalloids.
Boron silicon germanium arsenic antimony and tellurium are the most commonly recognized metalloids. List three properties of this substance. Metalloids exhibit some properties of metals as well as of non-metals.
Mostly solids at room temperature. They are also called semimetals. Metalloids are elements found between the metals and nonmetals on the periodic table of the elements.
These elements are shown in the following figure. Whether bonding with other metalloids or joining with metals or nonmetals the dance of a metalloid is fully determined by the rules set by electronegativity. Good conductors of heat and electricity.
The main difference between metals non-metals and metalloids are that metals are elements that are hard malleable fusible shiny ductile and good conductors. Metalloids are brittle solids that crumble to powder when struck. An appearance that is similar to metals.
Form alloys with other metals. Very brittle break easily. The nonmetals are brittle not malleable or ductile poor conductors of both heat and electricity and tend to gain electrons in chemical reactions.
Are good conductors of heat and electricity. Properties of Nonmetals. Properties of metals nonmetals metalloids.
Poor conductors of heat and electricity. Some nonmetals are liquids. Examples of nonmetals include oxygen chlorine and argon.
Metals have a shiny appearance non-metals have a dull appearance. Nonmetals pull the metals to them guiding them strictly like a conductor that leads a orchestras rehearsal. Metalloids are all solid at room temperature.
The difference in physical properties of Metals Nonmetals and Metalloids The difference in Properties of Metals Nonmetals and Metalloids State. Chemical Properties of Metalloids Their physical properties tend to be metallic but their chemical properties tend to be non-metallic. Nonmetals have very distinct properties than those of metals and metalloids.
The metalloids elements like boron silicon and antimony have some properties of metals and other properties of nonmetals. Usually less dense compared to metals. Malleability Metals can withstand hammering and can be shaped into thin sheets such as foils.
Terms in this set 23 malleable. They are more brittle than metals. These elements run diagonally across the Periodic Table.
The nonmetals in the periodic table. Physical Properties of metalloids Can be shiny or dull Conductivity of heat and electricity better than nonmetals but not as good as metals. Complete opposite of a metal.
Solid at room temperature. Trends in Metallic and Nonmetallic Character. Typically nonmetals have a dull appearance since they do not have a metallic appearance.
They can form alloys with other metals. Example non-metal elements are Hydrogen and Carbon. Metalloids are uniquely flexible partners.
Metalloids are useful in the semiconductor industry. When you think of nonmetals you might think of materials made of plastic or polystyrene. Non-metals do not have properties present in metals whereas metalloids are elements that have intermediate properties of both metals and non-metals.
Non-metals are typically brittle and are not easily molded into shapes. Metalloids are metallic-looking brittle solids that are either semiconductors or exist in semiconducting forms and have amphoteric or weakly acidic oxides. The oxidation number of an element in this group can range from 3 to -2 depending on the group in which it is located.
They are not lustrous. Nonmetals exhibit very different properties from metals. Have luster shiny metal.
Unlike metals nonmetals are not malleable or ductile. Metalloids are not malleable. Metals Nonmetals and Metalloids Chemistry 101 Periodic Table properties.
Nonmetals have properties opposite those of the metals. Metals are located in s p d and f blocks in the periodic table though non-metals is located in s and p blocks and metalloids are located in p block of the periodic table. The chemical elements can be broadly divided into metals metalloids and nonmetals according to their shared physical and chemical properties.
However metalloids have a shiny and dull appearance. Left of the stair step line. Hence they are also known as semi-metals.
Worksheets are metals and non metals chapter 3 metals nonmetals and metalloids teks lesson metals nonmetals and metalloids classifying metals nonmetals and metalloids nonfiction reading test metal detectors compounds formed between metal non metals metal natural science and technology grade 5. Compared to metals nonmetals are less dense. And have at least one basic oxide.
Property Metals Nonmetals Metalloids Luster Metals reflects light from their surface and can be polished for example in gold silver and copper.
The diagonals of a rectangle are of the same length and intersect one another The two diagonals of a rectangle intersect each other at different angles one acute angle and the other an obtuse. Determine the area of the dark blue section.
Rectangle Properties Of Quadrilaterals
The diagonals of a rectangle are.
Properties of diagonals of rectangle. A diagonal is defined as a line segment joining the two opposite vertices of a polygon. The diagonals are congruent. Perimeter L w L w.
Since the diagonals of a rectangle are congruent mo 26. In other words the point where the diagonals intersect cross divides each diagonal into two equal parts. The two diagonals are congruent same length.
Diagonals of a Rectangle The diagonals of the square divide the rectangle into two equal right angle triangle. The diagonals have the following properties. A rectangle has two pairs of equal sides.
Let O O O be the intersection of the diagonals of a rectangle. The fundamental properties of rectangles are. There exists a circumcircle centered at O O O whose radius is equal to half of the length of a diagonal.
Here you can read about diagonals the formula to calculate the number of diagonals diagonal of square formula diagonal of rectangle formula diagonals of rhombus and parallelogram and some fun properties of diagonals. Since the diagonals of a rectangle are congruent MO 26. The square has the following properties.
It has four right angles 90. To find the area of a rectangle just multiply the length times the width. Area L x w.
Finding length of MZ. Each diagonal of a rectangle is a diameter of its circumcircle. Students of 5th grade and 6th grade need to apply the property to find the missing measure.
To find MZ you must remember that the diagonals of a parallelogram bisect each otherRemember a rectangle is a type of parallelogram so rectangles get all of the parallelogram properties If MO 26 and the diagonals bisect each other then MZ ½26 13. The diagonals of a rhombus intersect at equal angles while the diagonals of a rectangle are equal in length. Presented here are printable worksheets based on the next important property of the rectangle - the diagonals of a rectangle are congruent and bisect each other.
Moreover the opposite sides of a rectangle are parallel and equal and diagonals bisect each other. A square can be considered a rectangle based on few properties. Area bounded by an arc and rectangle.
A rectangle is a quadrilateral with four right angles. This is one of the most important properties of parallelogram that is helpful in solving many mathematical problems related to 2-D geometry. A rectangle is closed flat shape having four sides and each angle equal to 90 degrees.
2L 2w. A rectangle whose two diagonals intersect each. A parallelogram is a special type of quadrilateral in which both pairs of opposite sides are parallelYes if you were confused about whether or not a parallelogram is a quadrilateral the answer is yes it is.
A rectangle is a quadrilateral The opposite sides are parallel and equal to each other Each interior angle is equal to 90 degrees The sum of all the interior angles is equal to 360 degrees The diagonals bisect each other Both the diagonals have the same. Every rhombus has two diagonals connecting pairs of opposite vertices. Unless the rectangle is a square and the angles formed by the intersection are not always the same measure size.
The opposite sides are parallel. Coordinate Quadrilateral Proof Tetraflexagon Coordinate Geometry. Since a rhombus is a parallelogram what four properties do rhombuses already possess.
In the figure above click show both diagonals then drag the orange dot at any vertex of the rectangle and convince yourself this is so. Properties of diagonals of rectangle. A rhombus is a parallelgram with 4 congruent sides.
Diagonals that are perpendicular and congruent. The diagonals bisect each other. Opposite sides are equal and parallel all angles are equal to 90 degrees diagonals bisect each other sum of all angles equal to 360 degrees.
Therefore not only does a rectangles diagonals bisect each other they bisect each other into four congruent segments. The length of Diagonal of a rectangle can be found by using pythagorus theorem in the anyone of the right-angle triangle formed by diagonalyou will find given formula of the length of diagonal of the rectangle. Finding length of mz.
What is the shape of rectangle. All the properties of a rectangle apply the only one that matters here is diagonals are congruent. Each diagonal bisects the other.
Properties of the diagonals. The figure formed by joining the midpoints of the sides of a rhombus is a rectangle and vice versa. All the properties of a rhombus apply the ones that matter here are parallel sides diagonals are perpendicular bisectors of each other and diagonals bisect the angles.
The area of a rectangle. Now lets explore rhombuses. The perimeter of a rectangle.
Properties of a rectangle. Thus all the angles in a rectangle are equal 3604 90. The properties of diagonals of rectangle is hereunder.
A square has all the properties of a. To find the perimeter of a rectangle just add up all the lengths of the sides. A rectangle with side lengths a a a and b b b is circumscribed as shown.