The ASA Postulate was contributed by Thales of Miletus Greek. What is the Angle-Side-Angle Postulate for Triangle Congruence.
Angle Side Angle Postulate For Proving Congruent Triangles Examples Powerpoints This Postulate States
The ASS Postulate does not exist because an angle and two sides does not guarantee that two triangles are congruent.
Angle side angle postulate. The postulate states that two triangles are similar if they have two corresponding angles that are congruent or equal in measure. Side-Angle-Side SAS Similarity Postulate. Angle-Angle-Side Postulate AAS The AAS Postulate says that if two angles and the non-included side of one triangle are congruent to two angles and the non-included side of a second triangle then the triangles are congruent.
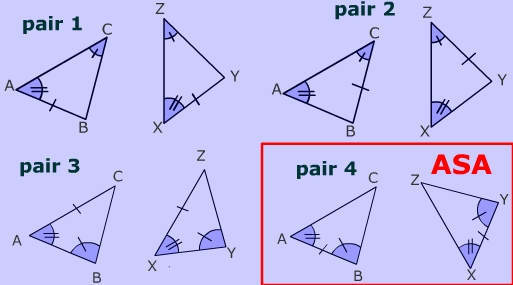
Angle side angle postulate ASA - If two angles and the included side of a triangle are congruent to two angles and the included side of another triangle then the two triangles are congruent by angle-side-angle postulate. This is very similar to the ASA Postulate above because it also has two angles and a side. The Side-Angle-Side postulate is just one of many postulates you can use to show two triangles are congruent.
The SAS rule states that. An included angle is an angle formed by two given sides. Side-Side-Side SSS Similarity Postulate.
Angle-Side-Angle Postulate ASA The ASA Postulate says that if two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle then the triangles are congruent. If two pairs of angles of two triangles are equal in measurement and the included sides are equal in length then the triangles are congruent. Lets say you have one triangle with angles that are 30 and 50 degrees and the side in between those two angles is 9 cm.
Prove the opposite sides and the opposite angles of a parallelogram are congruent. Angle angle side postulate AAS- If two angles and a non-included side of a triangle are congruent to two angles and the corresponding non-included side of another triangle then the two triangles are congruent by angle angle side postulate. This is why there is no Side Side Angle SSA and there is no Angle Side Side ASS postulate.
Using this postulate we no longer have to show that all three. Side Angle Side Postulate The SAS Postulate tells us If two sides and the included angle of a triangle are congruent to two sides and the included angle of another triangle then the two triangles are congruent. If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle then the triangles are congruent.
If two triangles have two congruent sides and a congruent non included angle then triangles are NOT NECESSARILLY congruent. If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle the triangles are congruent. The AAS Theorem says.
ABCD is a parallelogram. We can use the Angle Side Angle postulate to prove that the opposite sides and the opposite angles of a parallelogram are congruent Proof 4 Given. If a line through a triangle is parallel to one of the triangles sides the line.
Consider the following two triangles Delta ABC and Delta DEF We are given that begingathered BC EF hfill angle B angle E hfill. The included side is the side between the vertices of the two angles The following figure shows how ASA works. Angle-Angle-Side or AAS Congruence Postulate is a rule which can be used to prove the congruence of two triangles.
B E C F and AC DF Δ ABC Δ DEF by AAS. Worksheet Activity on the Angle Angle Side Postulate Example of Angle Angle Side Proof AAS ABC XYZ. The ASA Angle-Side-Angle postulate states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle then the triangles are congruent.
Side-Angle-Side is a rule used to prove whether a given set of triangles are congruent. This tutorial introduces you to the SAS postulate and shows you how to use it. Proving Triangles Congruent by ASA AAS and HL.
In most systems of axioms the three criteria SAS SSS and ASA are established as theorems. B E BC EF and C F ΔABC Δ DEF by ASA. HUG and LAB each have one angle measuring exactly 63.
Angle side angle theorem states that two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle. The Angle Angle Side postulate often abbreviated as AAS states that if two angles and the non-included side one triangle are congruent to two angles and the non-included side of another triangle then these two triangles are congruent. If two triangles have a congruent angle and the sides that create this angle are proportional the triangles are similar.
If all three corresponding sides of two triangles form the same proportion the triangles are similar. The Side Angle Side postulate often abbreviated as SAS states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle then these two triangles are congruent. Notice how it says non-included side meaning you take two consecutive angles and then move on to the next side in either direction.