0 2 and 2. Determining local extrema in which extrema represents both the maximum and minimum values of a function requires the first derivative.
 How To Find Local Extrema With The First Derivative Test Dummies
How To Find Local Extrema With The First Derivative Test Dummies
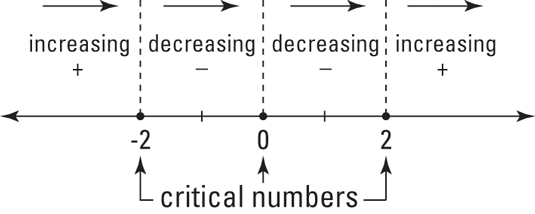
You divide this number line into four regions.
First derivative test for local extrema. Using the first derivative test to find relative local extrema. F x x 2 x 1. This calculus video tutorial provides a basic introduction into the first derivative test.
The biggest difference is that the first derivative test always determines whether a function has a local maximum a local minimum or neither. To the left of the eq x-3 eq the first derivative is positive and to the right of the point the first. Note that the first derivative test does not require the function to be differentiable at the point x0.
If that is the case you will have to apply the first derivative test to draw a conclusion. The following definitions make these terms more precise. Introduction to minimum and maximum points.
The point x0 is critical but not stationary the first derivative test can still be used to investigate the local extrema of the function. Take a number line and put down the critical numbers you have found. First Derivative Test for Local Extrema If the derivative of a function changes sign around a critical point the function is said to have a local relative extremum at that point.
If the derivative of a function changes sign around a critical point the function is said to have a local relative extrema at that point. To the left of 2 from 2 to 0 from 0 to 2 and to the right of 2. The First Derivative Test for Local Extrema When the graph of a function rises from left to right we say the function increases.
F xdfrac x2 x-1 f x x 1x2. Finding the relative extremum points of. Finding relative extrema first derivative test APCALC.
First Derivative Test for Local Extrema Let x c be a critical value of f x. If the derivative at this point is infinite or does not exist ie. Pick a value from each region plug it into the first derivative and note whether your result is positive or negative.
If the derivative c What is the First Derivative Test for Local Extrema. AP is a trademark registered and owned by the College Board which was not involved in the production of and does not endorse this site is a trademark registered and owned by the College Board which was not involved in the production of and does not endorse this site. F 1 2 is the local minimum value.
However the second derivative test fails to yield a conclusion when y is zero at a critical value. Consider the situation where c is some critical value of f in some open interval a b with f c 0. The first-derivative test depends on the increasingdecreasing test which is itself ultimately a consequence of the mean value theorem.
F left parenthesis x right parenthesis equals start fraction x squared divided by x minus 1 end fraction. Use the given graph of f x to estimate the. 43 Derivative Tests Filled Innotebook 3 November 05 2019 Nov 1223 PM Analyze the function using the first derivative test and the concavity test Nov 5852 AM a Increasing c Local Extrema d Inflection Points e Concave up b Decreasing f Concave down 2.
FUN4 EU FUN4A LO FUN4A2 EK Google Classroom Facebook Twitter. If f x changes its sign from - to around x c then f c is a local minimum. This lesson shows how to use the first derivative test in analyzing function f using f.
Finding relative extrema first derivative test. Suppose a function f is defined on some interval I. F x goes from negative to positive at x 1 the First Derivative Test tells us that there is a local minimum at x 1.
It is a direct consequence of the way the derivative is defined and its connection to decrease and increase of a function locally combined with the previous section. If f x changes its sign from to - around x c then f c is a local maximum. By using the f we can solve the critical number or critical point.
The Second Derivative Test for Local Extrema In addition to the first derivative test the second derivative can also be used to determine if and where a function has a local minimum or local maximum. Lets unpack it in a way that helps avoiding harmful omissions or mistakes. Its a long process but with hard work this can be done.
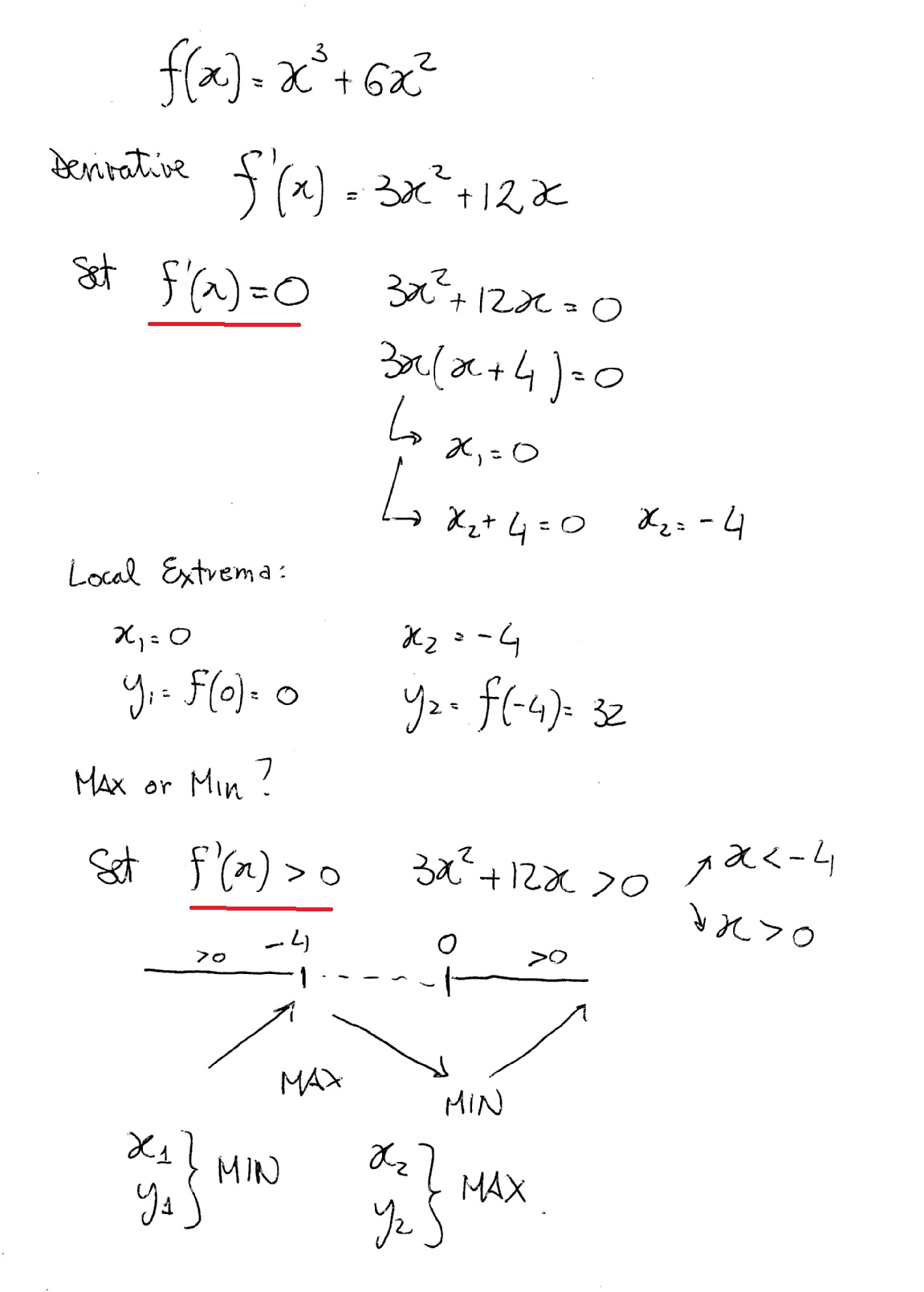
The first derivative test can be used to locate any relative extr. Use the first derivative test to find the local maximum and minimum values. This process is called the first derivative test.
Similarly when the graph falls from left to right we say the function decreases. Apply the First Derivative Test to identify all relative extrema of the function. If the derivative changes from positive increasing function to negative decreasing function the function has a local relative maximum at the critical point.