If any two angles are complementary the sine of one is the cosine of the other and vice versa. In a formula it is written simply as tan.
 Definition Ii Right Triangle Trigonometry Trigonometry Math 103 S Rook Ppt Download
Definition Ii Right Triangle Trigonometry Trigonometry Math 103 S Rook Ppt Download
To extending these definitions to functions whose domain is the whole projectively extended real line geometrical definitions using the standard unit circle ie a circle with radius 1 unit is often used.
Right triangle trigonometry definition. The Pythagorean Theorem proved using triangle similarity. The relation between the sides and angles of a right triangle is the basis for trigonometry. For example if you look up at something this angle is the angle between the ground and your line of site.
The tangent function along with sine and cosine is one of the three most common trigonometric functions. The Greeks focused on the calculation of chords while mathematicians in India created the earliest-known tables of values for trigonometric ratios such as sine. Right triangle definition The output of a trigonometric function is a ratio of the lengths of two sides of a right triangle.
Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. Chromosohm 43 Right Triangle Definitions of Trigonometric Functions Let be an acute angle of a right triangle. This identity is illustrated in Figure 5410.
In any right triangle the tangent of an angle is the length of the opposite side O divided by the length of the adjacent side A. Throughout history trigonometry has been applied in areas such as geodesy surveying celestial mech. Right triangle trigonometry word problems Get 3 of 4 questions to level up.
A line parallel to one side of a triangle divides the other two proportionally and conversely. Before calculators or computers were used they used various forms of trigonometric tables that contained the sides of triangles for different angles. That means that a right triangle can be formed with any two angles that add to π 2 π 2 in other words any two complementary angles.
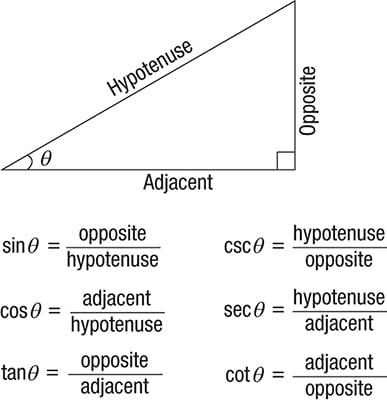
The sides of a right triangle are referenced as follows. Definition of sine and cosine using a right-angled triangle. A right triangle is a triangle in which one angle is a right angle.
For example the triangle contains an angle A and the ratio. Similarity Right Triangles and Trigonometry GSRTB4 Prove theorems about triangles. Right Triangle Trigonometry Joseph Sohm.
Opposite is opposite to the angle θ Adjacent is adjacent next to to the angle θ. If any two angles are complementary the sine of one is the cosine of the other and vice versa. Similarity Right Triangles and Trigonometry GSRTC6 Understand that by similarity side ratios in right triangles are properties of the angles in the triangle leading to definitions of trigonometric ratios for acute angles.
Here are some types of word problems applications that you might see when studying right angle trigonometry. Level up on the above skills and collect up to 400 Mastery points Start quiz. The reciprocal trigonometric ratios.
But the designations of opposite and adjacent can change depending on which angle youre referring to at the time. The sides adjacent to the right angle are called legs sides a a and b b. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.
There are six functions of an angle commonly used in trigonometry. So we may state a cofunction identity. The terms used to describe the sides of a right triangle are the hypotenuse the adjacent side and the opposite side as shown in the figure below.
Note that the angle of elevation is the angle up from the ground. The label hypotenuse always remains the same its the longest side. Their names and abbreviations are sine sin cosine cos tangent tan cotangent cot secant sec and cosecant csc.
These six trigonometric functions in relation to a right triangle are displayed in the figure. Sine Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle. The side opposite the right angle is called the hypotenuse side c c in the figure.
Right triangle trigonometry review Opens a modal Practice. The basic trig functions can be defined with ratios created by dividing the lengths of the sides of a right triangle in a specific order. This identity is illustrated in Figure 10.
The oldest definitions of trigonometric functions related to right-angle triangles define them only for acute angles. That means that a right triangle can be formed with any two angles that add to π 2 in other words any two complementary angles. Before getting stuck into the functions it helps to give a name to each side of a right triangle.
So we may state a cofunction identity. Note that the functions in the second row are the reciprocals of the corresponding functions in the first row. A right triangle can also be isoscelesif the two sides that include the right angle are equal in length AB and BC in the figure above A right triangle can never be equilateral since the hypotenuse the side opposite the right angle is always longer than either of the other two sides.
Similar triangles have been used throughout history to estimate distances that cannot be measured directly. The angle of depression is the angle that comes down from a straight horizontal. The six trigonometric functions of the angle are defined as follows.