Central Projection Matrix construction. When you have an angle bisector you also have two smaller triangles.
 Angle Bisector Theorem Wikipedia
Angle Bisector Theorem Wikipedia
So 4 1.
Triangle angle bisector theorem. Triangle angle calculator is a safe bet if you want to know how to find the angle of a triangle. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangles side is divided into by a line that bisects the opposite angle. The Angle-Bisector theorem involves a proportion like with similar triangles.
The angles 4 and 1 are corresponding angles. The angle bisector theorem tells us that the angle bisector divides the triangles sides proportionally. As you can see in the picture below the angle bisector theorem states that the angle bisector like segment AD in the picture below divides the sides of the a triangle proportionally.
In ΔABC AD is the internal bisector of BAC which meets BC at D. Extend C A to meet B E at point E. Case i Internally.
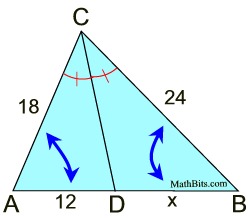
Angle BAD Angle DAC x. Whether you have three sides of a triangle given two sides and an angle or just two angles this tool is a solution to your geometry problems. Be sure to change the locations of the triangles vertices each time before you drag the slider.
To bisect an angle means to cut it into two equal parts or angles. What is the Angle Bisector theorem. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
How are the side-splitter theorem and the angle bisector theorem similar. According to the angle bisector theorem dfracBDDCdfracABAC. The following figure illustrates this.
Likewise the converse of this theorem holds as well. The picture below shows the proportion in action. In other words ABBD.
Further by combining with Stewarts Theorem it can be shown that. This applet accompanies the Triangle-Angle Bisector Theorem discovery activity given to you in class and attached here for your convenience Have fun with this. Triangle Angle Bisector Theorem.
Angle bisector of a triangle - Angle bisector theorem. Converting Decimals to Fractions. Finding missing angles in triangles - example.
In geometry the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle s side is divided into by a line that bisects the opposite angle. Get three colors for todays lesson 2 new lesson on notes Assign 154N Triangle Angle Bisector Theorem 3 quick quiz SmartGoal on ss int. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.
Conversely when a point D on the side BC divides BC in the ratio similar to the sides AC and AB then the angle bisector of A is AD. It equates their relative lengths to the relative lengths of the other two sides of the triangle. Triangle Angle Bisector Theoremnotebook May 09 2016 Intro to Geom for Monday 5916 seniors.
The angle bisector is a line that divides an angle into two equal halves each with the same angle measure. The internal external bisector of an angle of a triangle divides the opposite side internally externally in the ratio of the corresponding sides containing the angle. The only similarity between the side-splitter theorem and the angle bisector theorem is that both the theorems related the proportions of side lengths of the triangle.
Then According to Angle bisector theorem the ratio of the line segment BD to DC equals to the ratio of length of the side AB to AC. In the triangle ABC the angle bisector intersects side BC at the point D. 1 hand back papers.
The Angle Bisector Theorem If ABC is any triangle and AD bisects cuts in half the angle BAC then AB BD AC DC To show this is true we can label the triangle like this. The angle bisector theorem state that in a triangle the angle bisector partitions the opposite side of the triangle into two segments with a ratio that is the same as the ratio between the two sides forming the angle it bisects. It is these two.
The Angle-Bisector theorem states that if a ray bisects an angle of a triangle then it divides the opposite side into segments that are proportional to the other two sides. Draw B E A D. The Angle Bisector Theorem states that given triangle and angle bisector AD where D is on side BC then.
The angle bisector theorem states that an angle bisector divides the opposite side of a triangle into two segments that are proportional to the triangles other two sides.