Sum of interior angles p - 2 180 3060 p - 2 180 p - 2 frac3060180 p - 2 17. The following diagram shows the formula for the sum of interior angles of an n-sided polygon and the size of an interior angle of a n-sided regular polygon.
 Sum Of All Exterior Angles Of A Polygon
Sum Of All Exterior Angles Of A Polygon
The interior angles of a polygon always lie inside the polygon.

Formula for the interior angles of a polygon. The formula for calculating the sum of interior angles is n - 2 times 180circ where n is the number of. Sum of interior angles of n-sided polygon n x 180- 360 n-2 x 180. That will give you the missing angle.
Sum of Interior Angles Formula. The sum of the interior angles of a polygon is given by the product of two less than the number of sides of the polygon and the sum of the interior angles of a triangle. If n is the number of sides of a polygon then the formula is given below.
Interior angle sum of a pentagon 3 x 180 540. Sum of interior angles of a polygon with p sides is given by. Interior Angle Formula Interior Angle Formula Definition Examples Sum of Interior Angles.
Here is how the Sum of the interior angles of regular polygon calculation can be explained with given input values - 540 5-2180. Because the square can be made from two triangles. The interior angles in a triangle add up to 180.
Interior Angles of a Polygon Formula. Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o. Interior angles of a Regular Polygon 180n.
If you take a look at other geometry lessons on. Then add together all of the known angles and subtract that sum from the sum you calculated first. 2 question What is the formula for the sum of the interior angle measures of a polygon.
To find the sum of interior angles of a polygon multiply the number. To use this online calculator for Sum of the interior angles of regular polygon enter Number of sides n and hit the calculate button. Triangle 3 2 180.
If the polygon is regular - all its interior angles are equal - you can use. The sum of the measures of the interior angles of a convex polygon with n sides is. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.
N 2 180. The formula can be obtained in three ways. Total interior angles n - 2180 where n is the number of sides.
And for the square they add up to 360. Make sure each triangle here adds up to 180 and check that the pentagon s interior angles add up to 540 the interior angles of a pentagon add up to 540. First calculate the sum of all the interior angles of the polygon by using the formula n - 2 180 where n is the number of sides.
Sum of Interior Angles of a Polygon Formula Example Problems. The sum of interior angles in a triangle is 180. All the interior angles in a regular polygon are equal.
The sum of the interior angles of a regular polygon is 3060 0. Formula for interior angle of a polygon n - 2 180 where n is the number of sides of the polygon Now equate the formula to 5400 n - 2 180 5400 open bracket by multiply by 180 180n - 360 5400 180n 5400 360 180n 5760 n ⁵⁷⁶⁰₁₈₀ n 32 so the polygon has 32 sides. Interior and exterior angle formulas.
Scroll down the page for more examples and solutions on the interior angles of a polygon. Find the sum of the interior angles of a heptagon 7-sided Solution. To find the sum of the interior angles you multiply 3 by 180.
Find the number of sides in the polygon. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Let us discuss the three different formulas in detail.
Sum of angles of each triangle 180 Please note that there is an angle at a point 360 around P containing angles which are not interior angles of the given polygon. From the simplest polygon a triangle to the infinitely complex polygon with n n sides sides. Interior Angles of Regular Polygons Remember that the sum of the interior angles of a polygon is given by the formula Sum of interior angles 180 n 2 where n the number of sides in the polygon.
N5 S 3 Step 2. First all regular polygons can be inscribed in a circle.
Use this calculator to calculate properties of a regular polygon.

Area of regular polygon. In Euclidean geometry a regular polygon is a polygon that is equiangular and equilateral. Number of sides n. Equilateral and equal angles ie.
The area of any regular polygon is equal to half of the product of the perimeter and the apothem. Area of a Regular Polygon Formula Combine the number of sides n n and the measure of one side s s with the apothem a a to find the area A A of any regular polygon. Therefore the area of a regular polygon is given by.
You use the following formula to find the area of a regular polygon. By definition all sides of a regular polygon are equal in length. So whats the area of the hexagon shown above.
Now click the button Solve to get the regular polygon area Step 3. The area of any. Polygon area Sp.
Learn how to find the area of a regular polygon using the formula A12ap in this free math video tutorial by Marios Math Tutoring. Given the length of a side. Enter any 1 variable plus the number of sides or the polygon name.
How to use the formula to find the area of any regular polygon. Given the apothem inradius. The perimeter is the combined length of the outline of any two-dimensional figure.
Perimeter of a Regular Polygon. Calculate the area of a regular pentagon with side 12 cm and apothem of 75 cm. An apothem is also used sometimes to find the area of a regular polygon.
Area ratio SpSc Customer Voice. Enter the number of sides and side length in the input field Example. Given the radius circumradiusIf you know the radius distance from the center to a vertex see figure.
Shape with at least three sides. Equiangular is known as a regular polygon. The area of a regular n -gon with side s inscribed in a unit circle is.
Calculate from an regular 3-gon up to a regular 1000-gon. The procedure to use the area of regular polygon calculator is as follows. If the length of a side is s and there are n sides in a regular polygon then the perimeter is P ns.
Side length a. In the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon if the edge length is fixed. Polygons can be regular or irregular.
Regular polygons may be either convex or star. Circle area Sc. Area of regular polygon where p is the perimeter and a is the apothem.
Area of a regular polygon 1. Know the correct formula. A n s a 2 A n s a 2 Lets dive into the details.
We go through an example involving a regular pentagon inscrib. Calculates side length inradius apothem circumradius area and perimeter. Calculates the side length and area of the regular polygon inscribed to a circle.
We go through two exampl. If the angles are all equal and all the sides are equal length it is a regular polygon. Finding the area of regular polygon when the SIDE and APOTHEM are known.
Area of Regular Polygon Formula A polygon having equal sides ie. Area of Polygon n Apothem 2 tanπn When we dont know the Apothem we can use the same formula but re-worked for Radius or for Side. To find the area of a regular polygon you use an apothem a segment that joins the polygons center to the midpoint of any side and that is perpendicular to that side segment HM in the following figure is an apothem.
If you know the length. The area of a regular polygon is given in terms of the radius r of its inscribed circle and its perimeter p by displaystyle A tfrac 1 2cdot pcdot r This radius is also termed its apothem and is often represented as a. Where p the perimeter of the polygon sum of all the side lengths of a polygon.
Calculate the area of a regular polygon Last update on February 26 2020 080918 UTCGMT 8 hours. Finally the area of the regular polygon will be displayed. Apothem is a segment that joins the polygons center to the midpoint of any side and it is perpendicular to that side.
A 12. The apothem is a line segment that joins the polygons center to the midpoint of any side that is perpendicular to that side. Area of Polygon ½ n Radius 2 sin2 π n.
As the polygon is a pentagon having five sides where each side s measures 12 cm its perimeter p is 5 x s 5 x 12 60 cm Now as we know. Note that units of length are shown for. In order to find the area of a regular polygon we need to define some new terminology.
Calculating the Area 1. The apothem of a regular polygon is the shortest distance from the center point to one of the. Learn how to find the area of a regular polygon when only given the radius of the the polygon.
Regular polygons inscribed to a circle 1-10 69.
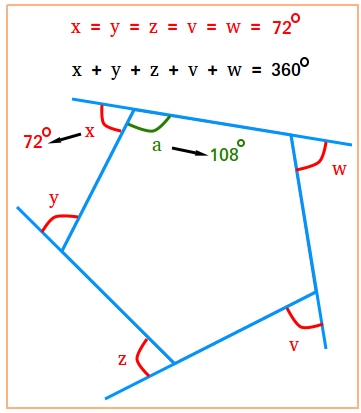
For example the interior angles of a pentagon always add up to 540 no matter if it regular or irregular convex or concave or what size and shape it is. Therefore the sum of the interior angles of the polygon is given by the formula.
Interior Angles Of A Polygon Equation
Its interior angles add up to 3 180 540 And when it is regular all angles the same then each angle is 540 5 108 Exercise.

Formula for calculating interior angles of a polygon. Interior angle of regular polygon calculator uses Interior angle of regular polygon Number of sides-2180Number of sides to calculate the Interior angle of regular polygon The interior angle of regular polygon can be defined as an angle inside a shape and calculated by dividing the sum of all interior angles by the number of congruent sides of a regular polygon. The sum of the interior angles of a polygon is given by the formula. If a polygon has p sides then Sum of interior angles p - 2 180 Sum of Interior Angles of a Regular Polygon and Irregular Polygon.
Since every triangle has interior angles measuring 180 180 multiplying the number of dividing triangles times 180 180 gives you the sum of the interior angles. All the interior angles in a regular polygon are equal. Interior angle sum of a pentagon 3 x 180 540 If the polygon is regular - all its interior angles are equal - you can use the result of the angle sum above to calculate the size of each angle.
Sum of Interior Angles Formula This formula allows you to mathematically divide any polygon into its minimum number of triangles. The sum of the measures of the interior angles of a polygon with n sides is n 2180. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.
S n 2 180 S n - 2 180. Where n Number of sides of a polygon degrees Use our below online interior angles of a polygon calculator to find the interior angles of polygon by entering the number of sides in the input box and then click calculate button to find the answer. First calculate the sum of all the interior angles of the polygon by using the formula n - 2180 where n is the number of sides.
The formula for calculating the sum of interior angles is n - 2 times 180circ where n is the number of. Then add together all of the known angles and subtract that sum from the sum you calculated first. Interior and exterior angle formulas.
The formula for each interior angle of a regular polygon is 180 n - 2 n where n the number of sides Using the strategy of partition or dissection the areas of these regular polygons can be found by adding together the areas of all of the congruent triangles formed by the. We discuss regular and nonregular. N 2 180.
Interior Angle Formula Where A is the sum of all interior angles n is the total number of sides of the polygon. The sum of the interior angles of a polygon is given by the product of two less than the number of sides of the polygon and the sum of the interior angles of a triangle. The sum of interior angles in a triangle is 180.
The following diagram shows the formula for the sum of interior angles of an n-sided polygon and the size of an interior angle of a n-sided regular polygon. Triangle 3 2 180. Sum of the Interior Angles of a Polygon 180 n-2 degrees Interior Angles of a Polygon Formula The interior angles of a polygon always lie inside the polygon.
Scroll down the page for more examples and solutions on the interior angles of a polygon. How to Calculate the Area of a Regular Polygon - dummies Remember. Find the sum of the interior angles of a heptagon 7-sided Solution.
To find the sum of interior angles of a polygon multiply the number. Interior angle of regular polygonSum of the interior angles of regular polygonNumber of sides GO Area of a regular polygon when length of side is given Area of regular polygonSide2Number of sides4tanpi180Number of sidespi GO. The sum of the measures of the interior angles of a convex polygon with n sides is.
The sum of the measures of the interior angles of a convex n-gon is n - 2 180 The measure of each interior angle of a regular n-gon is 1n n - 2 180. That will give you the missing angle. Learn how to find the Interior and Exterior Angles of a Polygon in this free math video tutorial by Marios Math Tutoring.
Formula to calculate interior angles of a polygon is given by. Make sure each triangle here adds up to 180 and check that the pentagons interior angles add up to 540 The Interior Angles of a Pentagon add up to 540. The interior angles of any polygon always add up to a constant value which depends only on the number of sides.