30 60 Degree Right Triangles

A 30-60-90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees. A 30-60-90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees.

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

This lesson is going to examine one kind of right triangle which is a triangle that has exactly one right or 90 degree angle.

30 60 degree right triangles. The 306090 triangle is the only right triangle whose angles are in an arithmetic progression. The other is the isosceles right triangle. Any triangle of the form 30-60-90 can be solved without applying long-step methods such as the Pythagorean Theorem and trigonometric functions.

The sine and cosine of 30 to find out the others sides lengths. The fact that the remaining leg AD has length 3 follows immediately from the Pythagorean theorem. If you look at the 306090-degree triangle in radians it translates to the following.

A 30-60-90 degree triangle has angle measures of 30 60 and 90. If you are familiar with the trigonometric basics you can use eg. A 30-60-90 triangle is a particular right triangle because it has length values consistent and in primary ratio.

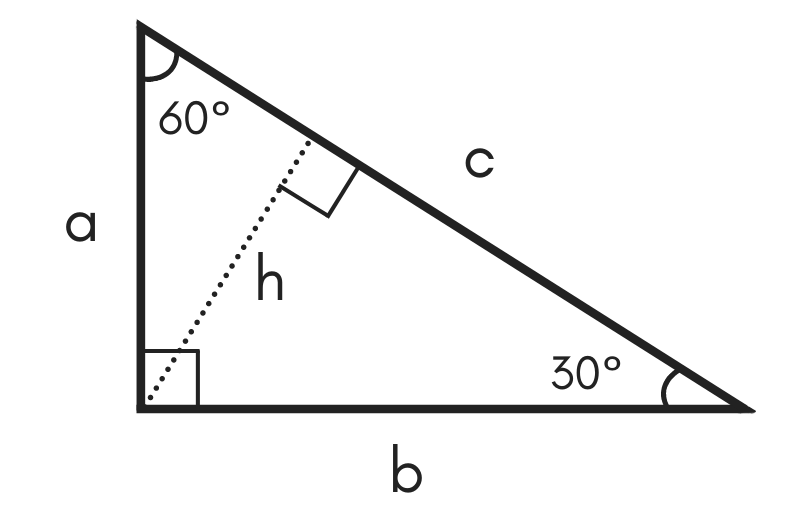
Thus in this type of triangle if the length of one side and the sides corresponding angle is known the length of the other sides can be determined using the above ratio. Bc sin 60 32 so b c32 a3. The 30 60 90 degree triangle is in the shape of half an equilateral triangle cut straight down the middle along its altitude.

The triangle is special because its side lengths are always in the ratio of 1. One is the 30-60-90 triangle. This is an isosceles right triangle.

The 30-60-90 refers to the angle measurements in degrees of this type of special right triangle. Because it is a special triangle it also has side length values which are always in a consistent relationship with one another. They have to add up to 180 30-60-90 triangle.

45-45-90 and 30-60-90 Triangles This page summarizes two types of right triangles which often appear in the study of mathematics and physics. THERE ARE TWO special triangles in trigonometry. Because it is a special triangle it also has side length values which are always in a consistent relationship with one another.

A 30-60-90 triangle is a unique right triangle. It is an equilateral triangle divided in two on its center down the middle along with its altitude. Also if you know two sides of the triangle you can find the third one from the Pythagorean theorem.

All 30-60-90 triangles have sides with the same basic ratio. Because the angles are always in that ratio the sides are also always in the same ratio to each other. Properties of a 30-60-90 Right Triangle A special kind of triangle.

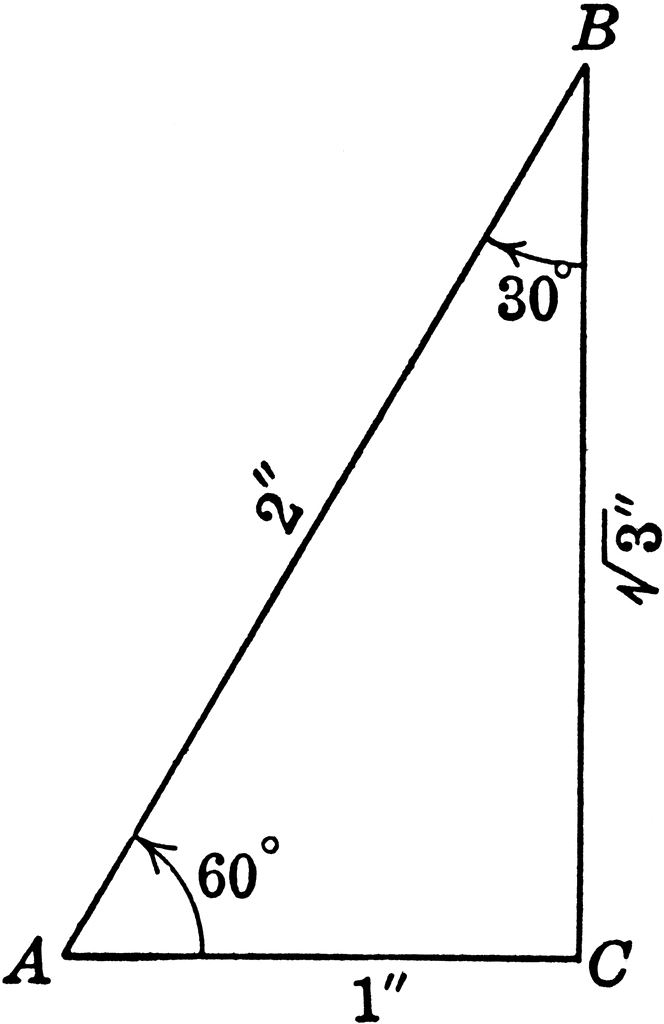
Then ABD is a 306090 triangle with hypotenuse of length 2 and base BD of length 1. The figure illustrates the ratio of the sides for the 30-60-90-degree triangle. Ac sin 30 12 so c 2a.

A 30-60-90 right triangle literally pronounced thirty sixty ninety is a special type of. Because it is a special triangle it also has side length values which are always in a consistent relationship with one another. One of these right triangles is named a 45-45-90 triangle where the angles in the triangle are 45 degrees 45 degrees and 90 degrees.

A 30-60-90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees. And you can also figure out the measures of this triangle although its not going to be a right triangle. This specific kind is a 30-60-90 triangle which is just a right.

The key characteristic of a 30-60-90 right triangle is that its angles have measures of 30 degrees π6 rads 60 degrees π3 rads and 90 degrees π2 rads. In this type of right triangle the sides corresponding to the angles 30-60-90 follow a ratio of 1 32. Since this is a 30-60-90 right triangle we know that the sides exist in the proportion 1.

It has angles of 30 60 and 90 and sides in the ratio of The following figure shows an example. The side opposite the 30º angle is the shortest and the length of it is usually labeled as. Two of the most common right triangles are 30-60-90 and the 45-45-90 degree triangles.

Use the same. This one is 30 90 so this other side right over here needs to be 60 degrees. This triangle right over here you have 30 you have 90 so this one has to be 60 degrees.

A 30-60-90 triangle is a right triangle with angle measures of 30º 60º and 90º the right angle. 45-45-90 and 30-60-90 degree triangles This video discusses two special right triangles how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side and then does a few examples using them. Get acquainted with this triangle by doing a couple of problems.

Properties Of A 30-60-90 Triangle A 30-60-90 right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees. A 30-60-90 triangle is a special right triangle whose angles are 30º 60º and 90º. Special Right Triangles in Geometry.

They are special because with simple geometry we can know the ratios of their sides.

30 60 90 Triangle Explanation Examples